Time Series Analysis - Weighted (Unequal) Moving Average Method

Time Series Analysis - Weighted (Unequal) Moving Average Method

• 1.
  Weighted (Unequal) Moving AverageMethod Sundar B. N. Assistant Professor
• 2.
  Methods of MovingAverage Equal Weight(Simple)Moving Average Method Weighted (unequal) Moving Average Method
• 3.
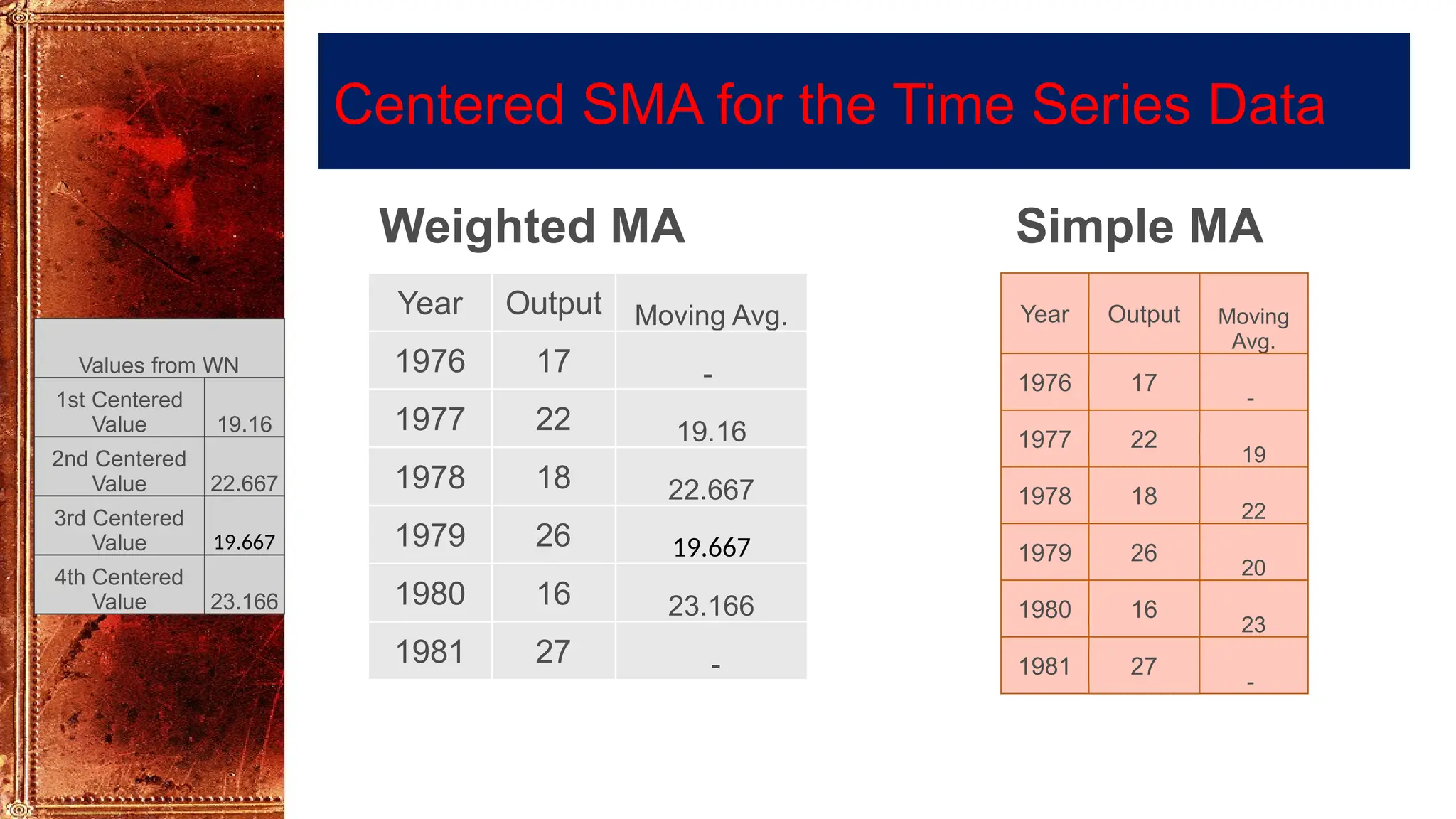
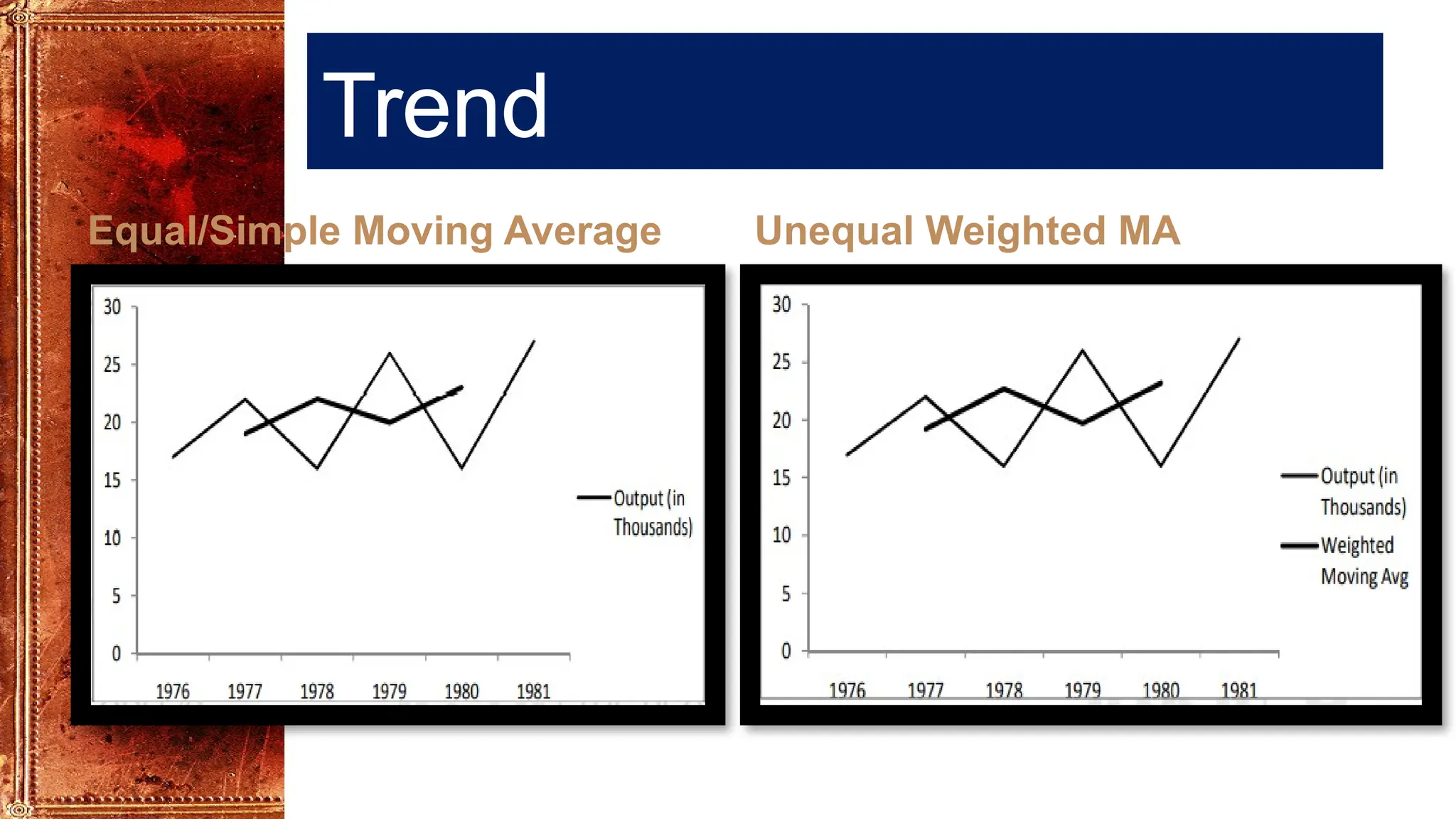
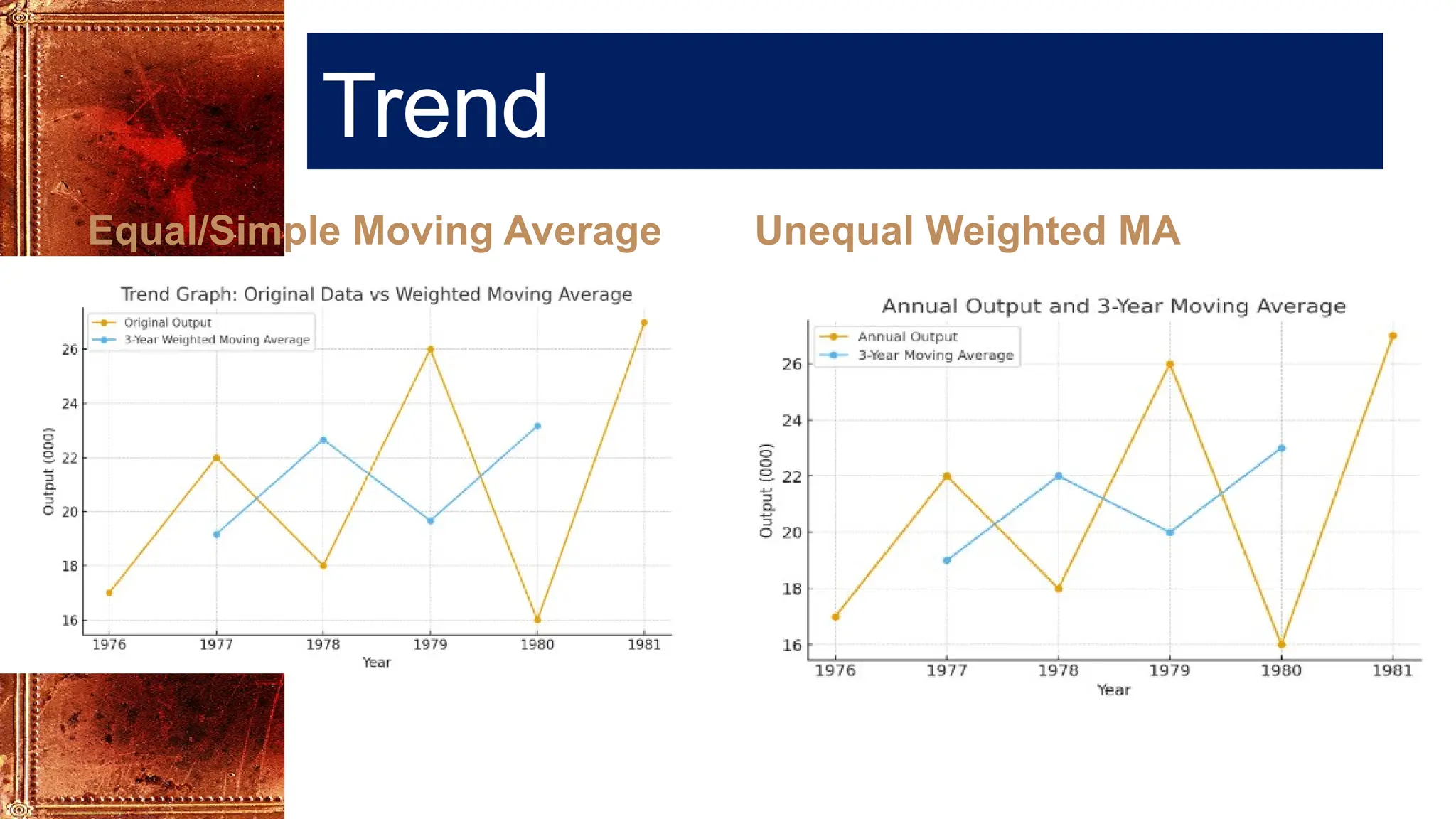
  Weighted (Unequal) MovingAverage Method  The simple moving average method is not generally recommended for measuring trend although it can be useful for removing seasonal variation.  It may also not lie close to the latest values. Therefore, the weighted (unequal) moving averages method is used.  In this method, instead of giving equal weights to all values, unequal weights are given in such a way that all the weights are positive and their sum is equal to 1.
• 4.
  Formula If wi denotesthe weight of the ith observation, the weighted moving average value yt is given by Smoothened trend values as yt = (xt-1 + 2xt + 3xt+1)/6
• 5.
  Procedure for Gettingthe Smoothened Trend Values 1.Calculate the weighted average of the first m values given in time series as explained above. 2. Now discard the first value and include the next one and take the average of the next m values by following the weight structure given in equation (2). 3. Repeat this process till all values are exhausted. These steps yield a new time series of m-period weighted moving averages and the weighted moving average values are given in the following table:
• 6.
  Problem Compute the 3-yearsweighted moving averages for the time series of annual output of a factory for the period 1976 to 1981 Annual output of a factory from 1976 to 1981 Year 1976 1977 1978 1979 1980 1981 Output (000) 17 22 18 26 16 27
• 7.
  Solution Generally, the mostrecent observation receives the largest weight and the weights decrease for older data values. For the data given in Example 1, suppose we give 3 times more weight to the most recent observation than the first observation and 2 times more weight to the second observation. Then the weights for each year in every 3-year period are: W₁=1/6 W₂=2/6 W₃=3/6 After assigning the weights as above, we get the smoothened trend values as yt = (xt-1 + 2xt + 3xt+1)/6
• 8.
  Working Note 1st Value 1/6(17)+2/6(22)+3/6(18) =2.833+7.333+9 =19.16 2nd Value1/6(22)+2/6(18)+3/6(26) =3.667+6+13 =22.667 3rd Value 1/6(18)+2/6(26)+3/6(16) =3+8.667+8 =19.667 th Output from1976 to 1981 Year Output 1976 17 1977 22 1978 18 1979 26 1980 16 1981 27
• 9.
  Working Note yt =(xt-1 + 2xt + 3xt+1)/6 1st Value =(17-1+2*22+3*18+1)/6 =(16+44+55)/6 =19.1667 2nd Value =(22-1+2*18+3*26+1)/6 =(21+36+79)/6 =22.667 3rd Value =(18-1+2*26+3*16+1)/6 =(17+52+49)/6 Output from1976 to 1981 Year Output 1976 17 1977 22 1978 18 1979 26 1980 16 1981 27
• 10.
  Centered SMA forthe Time Series Data Weighted MA Simple MA Year Output Moving Avg. 1976 17 - 1977 22 19.16 1978 18 22.667 1979 26 19.667 1980 16 23.166 1981 27 - Values from WN 1st Centered Value 19.16 2nd Centered Value 22.667 3rd Centered Value 19.667 4th Centered Value 23.166 Year Output Moving Avg. 1976 17 - 1977 22 19 1978 18 22 1979 26 20 1980 16 23 1981 27 -
• 11.
  Trend Equal/Simple Moving AverageUnequal Weighted MA
• 12.
  Trend Equal/Simple Moving AverageUnequal Weighted MA
• 13.
  Reference  Bhardwaj, R.S. (2009). Business Statistics. Excel Books India.  Shukla, G. K.; Trivedi, Manish (2017). “Unit- 13 Trend Component Analysis. IGNOU